1. Mở đầu

Lý thuyết xác suất là một phân nhánh của toán học liên quan đến việc phân tích, đánh giá các sự kiện ngẫu nhiên. Một trong những ngành mà lý thuyết xác suất được sử dụng rất nhiều là truyền thông (communication). Bài viết này sẽ trình bày một ứng dụng của lý thuyết xác suất trong việc đánh giá độ tin cậy của giao thức ALOHA.

Một chút về lịch sử: ALOHA là hệ thống mạng máy tính đầu tiên, được phát triển ở đại học Hawaii. ALOHA được đưa vào sử dụng năm 1971, trở thành hình mẫu đầu tiên của mạng không dây truyền gói dữ liệu (wireless packet data network).

2. Tại sao giao thức ALOHA được coi là thiếu ổn định?

Trong phần này, dựa trên lý thuyết xác suất, chúng ta sẽ chứng minh sự thiếu ổn định của giao thức ALOHA.

Xét một communications facility ở đó: chia thời gian thành các slot có cùng period, số lượng bản tin đến tại thời điểm đầu mỗi slot n = 1, 2, … là các biến ngẫu nhiên độc lập với nhau và phân bố đồng dạng (indepedent and identically distributed). Đặt ai = P{có i bản tin đến} và giả sử rằng a0 + a1 < 1, tức là vẫn có khả năng nhiều hơn 2 bản tin sẽ đến. Mỗi bản tin đến sẽ được truyền đi tại cuối slot mà nó đến. Nếu có đúng một bản tin được truyền đi, việc truyền tin thành công và bản tin sẽ rời khỏi hệ thống. Trong trường hợp ngược lại, nếu cuối một slot nào đó, ít nhất 2 bản tin đồng thời được truyền, sẽ xảy ra xung đột và những bản tin này vẫn ở lại trong hệ thống. Khi một bản tin gặp xung đột, nó sẽ độc lập với các bản tin khác truyền đi tại cuối slot tiếp theo với xác suất p. Ta sẽ chứng minh hệ thống như vậy sẽ không ổn định theo nghĩa: số lượng các lần truyền tin thành công là hữu hạn, với xác suất là 1.

Đặt Xn là số lượng bản tin trong hệ thống tại bắt đầu slot thứ n. Để ý rằng {Xn, n > = 0} là một chuỗi Markov. Đưa vào một biến Ik như sau:

**Ik = 1**, nếu lần đầu tiên chuỗi rời trạng thái k, nó sẽ đi trực tiếp sang trạng thái k-1. **Ik = 0** trong các trường hợp còn lại, bao gồm cả trường hợp hệ thống không bao giờ ở trạng thái k. Lấy ví dụ, nếu chuỗi Markov là 0, 1, 3, 4… thì I3 = 0 do khi chuỗi rời khỏi trạng thái 3 thì nó sẽ đi sang trạng thái 4, không phải trạng thái 2. Ngược lại, nếu chuỗi là 0, 3, 3, 2, … thì I3 = 1 vì ở lần đầu tiên nó đi ra khỏi trạng thái 3 thì nó sẽ sang trạng thái 2. Hiểu một cách đơn giản, biến Ik là một biến xác định tại trạng thái k, hệ thống có gửi được bản tin nào đi không, nếu gửi được thì hệ thống nhảy sang trạng thái k-1 và biến Ik nhận giá trị 1 (true).

Bây giờ ta tính giá trị trung bình (mean) sau:

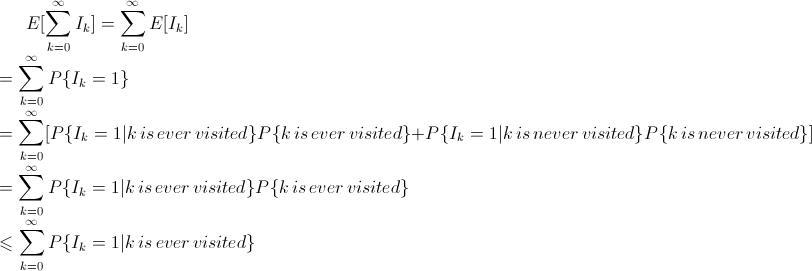
Bây giờ, P{Ik = 1 | k is ever visited} là xác suất khi rời khỏi trạng thái k, trạng thái tiếp theo sẽ là k-1. Đây là xác suất có điều kiện của sự kiện: chuyển trạng thái từ k sang k-1, biết rằng hệ thống sẽ không quay trở lại trạng thái k. Do đó:

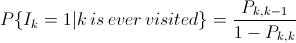
Ở đây, P{i,j} là xác suất của chuỗi Markov chuyển từ trạng thái i sang trạng thái j. Ta tính P{k,k-1} như sau: nhận thấy nếu có k bản tin ở đầu một slot thì sẽ có k-1 bản tin ở đầu slot tiếp theo nếu không có bản tin nào đến ở slot đó và chỉ có đúng một trong số k bản tin được truyền đi. Như vậy:

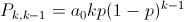
Đối với P{k,k}: nếu có k bản tin ở đầu một slot thì sẽ có k bản tin ở đầu slot tiếp theo nếu:

• không có bản tin nào đến và không xảy ra trường hợp: chỉ có đúng một trong số k bản tin được truyền đi. Tức là có thể không có bản tin nào truyền đi, như vậy vẫn chỉ có k bản tin. Hoặc là có 2 bản tin trở lên được truyền đi, nhưng như thế lại có xung đột và các bản tin này không được truyền và vẫn nằm nguyên trong hệ thống.

• có đúng một bản tin đến (và nó sẽ tự động được truyền đi) và không có bất cứ bản tin nào trong số k bản tin được truyền.

Đưa vào công thức, ta có:

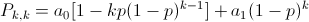
Tổng kết lại, ta có:

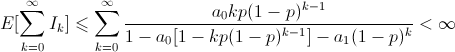
Trong công thức trên, để ý khi k đủ lớn, mẫu số của biểu thức sẽ hội tụ về 1-a0, còn trên tử số ta có:

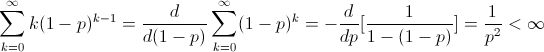
Do đó, giá trị trung bình (mean) của tổng tất cả Ik sẽ nhỏ hơn vô cùng. Điều đó chứng tỏ, tổng tất cả các Ik sẽ nhỏ hơn vô cùng với xác suất là 1 (vì ngược lại, nếu có xác suất dương là tổng này có thể bằng vô cùng, thì giá trị trung bình của nó sẽ phải là vô cùng). Như vậy, với xác suất là 1, sẽ chỉ có hữu hạn trạng thái mà chuỗi Markov có thể rời khỏi nhờ truyền bản tin thành công. Cũng có nghĩa là, sẽ có một số nguyên hữu hạn N nào đó, mà khi có ít nhất N bản tin trong hệ thống, sẽ không thể có truyền tin thành công nào nữa. Xác suất có ít nhất 2 bản tin đến là dương, trong trường hợp đó, hệ thống sẽ không có bản tin nào truyền đi cả, và số lượng bản tin sẽ tăng lên ít nhất 2 bản tin. Vậy nên, hệ thống cuối cùng sẽ đạt đến trạng thái có ít nhất N bản tin ở trên, và không thể có truyền tin thành công nữa.

Vậy là ta đã thấy, giao thức ALOHA, trên phương diện lý thuyết xác suất, không ổn định về đảm bảo truyền tin thành công.

Tài liệu tham khảo

1. Introduction to Probability Models - Sheldon Ross