Giới thiệu

Quy hoạch động là một trong những kĩ thuật lập trình cơ bản được sử dụng khá nhiều trong các cuộc thi lập trình. Ý tưởng về cơ bản rất đơn giản: để giải một bài toán, chúng ta đi giải các bài toán con, sau đó tổng hợp các lời giải đó lại thành lời giải của bài toán ban đầu. Trong một số bài toán, nếu không sử dụng quy hoạch động, rất nhiều bài toán con sẽ bị tính lặp đi lặp lại. Quy hoạch động sẽ tìm cách để giải mỗi bài toán con đúng 1 lần để giảm thiểu số lần tính toán. Một khi lời giải cho một bài toán con đã có, chúng ta lưu lại và lần tiếp theo cần lời giải đó, chúng ta chỉ cần tìm lại.

Quy hoạch động được sử dụng rất nhiều trong các thuật toán khác, ví dụ như: thuật toán Dijkstra tìm đường đi ngắn nhất, Knapsack, Nhân ma trận theo chuỗi (Chain matrix multiplication), thuật toán Floyd-Warshall tìm đường đi ngắn nhất giữa mọi cặp đỉnh trong đồ thị (đã có bài viết giới thiệu về thuật toán này).

Trong bài viết này, chúng ta sẽ cùng đi qua một số ví dụ sử dụng quy hoạch động trên TopCoder.

Ví dụ 1: ZigZag

A sequence of numbers is called a zig-zag sequence if the differences between successive numbers strictly alternate between positive and negative. The first difference (if one exists) may be either positive or negative. A sequence with fewer than two elements is trivially a zig-zag sequence.

For example, 1,7,4,9,2,5 is a zig-zag sequence because the differences (6,-3,5,-7,3) are alternately positive and negative. In contrast, 1,4,7,2,5 and 1,7,4,5,5 are not zig-zag sequences, the first because its first two differences are positive and the second because its last difference is zero.

Given a sequence of integers, sequence, return the length of the longest subsequence of sequence that is a zig-zag sequence. A subsequence is obtained by deleting some number of elements (possibly zero) from the original sequence, leaving the remaining elements in their original order.

{ 1, 7, 4, 9, 2, 5 }

Returns: 6

The entire sequence is a zig-zag sequence.

{ 1, 17, 5, 10, 13, 15, 10, 5, 16, 8 }

Returns: 7

There are several subsequences that achieve this length. One is 1,17,10,13,10,16,8.

{ 44 }

Returns: 1

{ 1, 2, 3, 4, 5, 6, 7, 8, 9 }

Returns: 2

{ 70, 55, 13, 2, 99, 2, 80, 80, 80, 80, 100, 19, 7, 5, 5, 5, 1000, 32, 32 }

Returns: 8

{ 374, 40, 854, 203, 203, 156, 362, 279, 812, 955, 600, 947, 978, 46, 100, 953, 670, 862, 568, 188, 67, 669, 810, 704, 52, 861, 49, 640, 370, 908, 477, 245, 413, 109, 659, 401, 483, 308, 609, 120, 249, 22, 176, 279, 23, 22, 617, 462, 459, 244 }

Returns: 36

Bài toán này là một dạng của bài toán tìm xâu dài nhất thoả mãn một điều kiện nào đó, ví dụ như tăng dần, giảm dần… Cách làm quy hoạch động là như sau: duyệt từ trái sang phải, tìm xâu dài nhất kết thúc tại phần tử đang xét. Xâu dài nhất này được tính dựa trên các bài toán con phía trước:

• Xem có thể thêm phần tử hiện tại vào các xâu dài nhất két thúc bằng các phần tử phía trước không.

• Chọn xâu dài nhất có thể trong các xâu thoả mãn.

Sau đây là đoạn code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

#include <iostream>
#include <cmath>
#include <vector>
using namespace std;

class ZigZag{
public:
  int longestZigZag(vector<int> sequence);
};

int ZigZag::longestZigZag(vector<int> sequence){
  int n = sequence.size();
  int f[n];
  bool isUp[n]; // check if in the longest sequence up to i-th member, we are going up or down
  for (int i = 0 ; i < n ; i++){
      f[i] = 1;
      for(int j = 0; j < i; j++){
          //special case
          if(j == 0 ){
              f[i] = 2;
              isUp[i] = sequence[i] > sequence[0];
          }
          if(isUp[j] == true && sequence[j] > sequence[i]){
              if(f[i] < f[j] + 1){
                  f[i] = f[j] + 1;
                  isUp[i] = false;
              }
          }
          if(isUp[j] == false && sequence[j] < sequence[i]){
              if(f[i] < f[j] + 1){
                  f[i] = f[j] + 1;
                  isUp[i] = true;
              }
          }
      }
  }

  return f[n-1];
}

Ví dụ 2: AvoidRoads

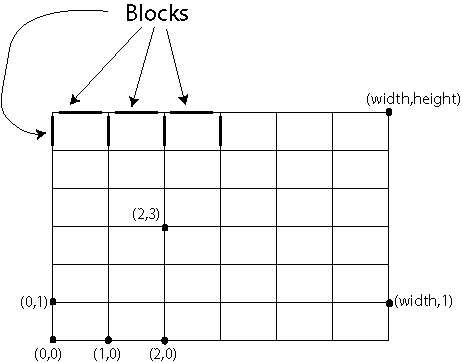
In the city, roads are arranged in a grid pattern. Each point on the grid represents a corner where two blocks meet. The points are connected by line segments which represent the various street blocks. Using the cartesian coordinate system, we can assign a pair of integers to each corner as shown below.

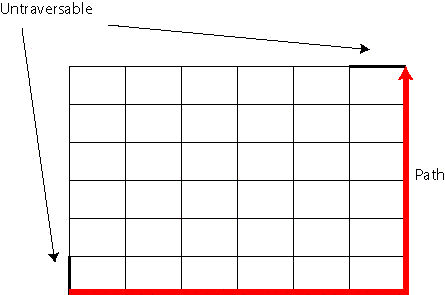
You are standing at the corner with coordinates 0,0. Your destination is at corner width,height. You will return the number of distinct paths that lead to your destination. Each path must use exactly width+height blocks. In addition, the city has declared certain street blocks untraversable. These blocks may not be a part of any path. You will be given a String[] bad describing which blocks are bad. If (quotes for clarity) “a b c d” is an element of bad, it means the block from corner a,b to corner c,d is untraversable. For example, let’s say width = 6 length = 6 bad = {“0 0 0 1”,“6 6 5 6”} The picture below shows the grid, with untraversable blocks darkened in black. A sample path has been highlighted in red.

Examples

6

6

{“0 0 0 1”,“6 6 5 6”}

Returns: 252

Example from above.

1

1

{}

Returns: 2

Four blocks aranged in a square. Only 2 paths allowed.

35

31

{}

Returns: 6406484391866534976

Big number.

2

2

{“0 0 1 0”, “1 2 2 2”, “1 1 2 1”}

Returns: 0

Vẫn trên tư tưởng quy hoạch động, dễ thấy ta cần duyệt từ đỉnh (0,0). Số lượng đường đi đến đỉnh (i,j) sẽ dựa trên số lượng đường đi đến đỉnh (i-1,j) và đỉnh (i, j-1). Chú ý nếu đường đi từ (i-1,j) hoặc (i, j-1) đến (i,j) bị chặn thì ta sẽ không tính đoạn đường đó nữa.

Sau đây là đoạn code (C++):

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

#include <iostream>
#include <vector>
#include <string>
#include <sstream>
#include <cmath>
#include <algorithm>

using namespace std;

class AvoidRoads{
public:
  long numWays(int width, int height, vector<string> bad);
};

long AvoidRoads::numWays(int width, int height, vector<string> bad){
  bool badVertical[width+1][height+1];
  bool badHorizontal[width+1][height+1];

  for(int i = 0; i <= width; i++){
      for(int j = 0 ; j <= height; j++){
          badVertical[i][j] = false;
          badHorizontal[i][j] = false;
      }
  }

  for(int i = 0; i< bad.size(); i++){
      stringstream temp(bad[i]);
      int x, y, z,  t;
      temp >> x >> y >> z >> t;
      if(abs(z - x) ==1){
          badHorizontal[min(x,z)][y] = true;
          cout << "bad Horizontal at: " << min(x,z) << ", " << y << "\n";
      }
      else if(abs(t - y) == 1){
          badVertical[x][min(y,t)] = true;
          cout << "bad Vertical at: " << x << ", " << min(y,t) << "\n";
      }
  }

  long res [width+1][height+1];
  res[0][0] = 1;
  for(int i = 0; i<= width; i++ ){
      for(int j = 0; j <= height; j++){
          //don't override the base case
          if((i == 0) && (j == 0)){
              continue;
          }

          long temp = 0;
          if(i>0 && !badHorizontal[i-1][j] ) {
              temp += res[i-1][j];
          }
          if(j>0 && !badVertical[i][j-1]){
              temp += res[i][j-1];
          }
          cout << "temp = " << temp << "\n";
          res[i][j] = temp;
          cout << "Ways to (" << i << "," << j << ") is: " << res[i][j] << "\n";
      }
  }
  return res[width][height];
}

Kết luận

Hi vọng qua 2 ví dụ trên, bạn đã phần nào có được tư tưởng quy hoạch động. Về cơ bản, chúng ta chỉ cần đi đến được cách tính bài toán hiện tại dựa vào các bài toán con trước đó là 90% công việc đã xong. Hãy luyện tập thêm để chiến đấu tại TopCoder!

Tham khảo

1. TopCoder Graph Tutorial
2. ZigZag
3. AvoidRoad